医学统计学学习笔记
03.常见的统计学概念混淆
发病率vs患病率
发病率(incidence rate)表示在观察期间内,可能发生某病的人群中发生该病的频率
患病率(prevalence rate)表示某特定时间内一定人群中某疾病新旧病例所占比例


死亡率vs病死率
死亡率:在一定时期内(通常为1年),在一定人群中死于某疾病(或死亡于所有原因)的人占总人口比例
病死率:表示一定时期内(通常为1年),某患病的全部病人中印该病死亡的人所占比例
生存率vs生存概率
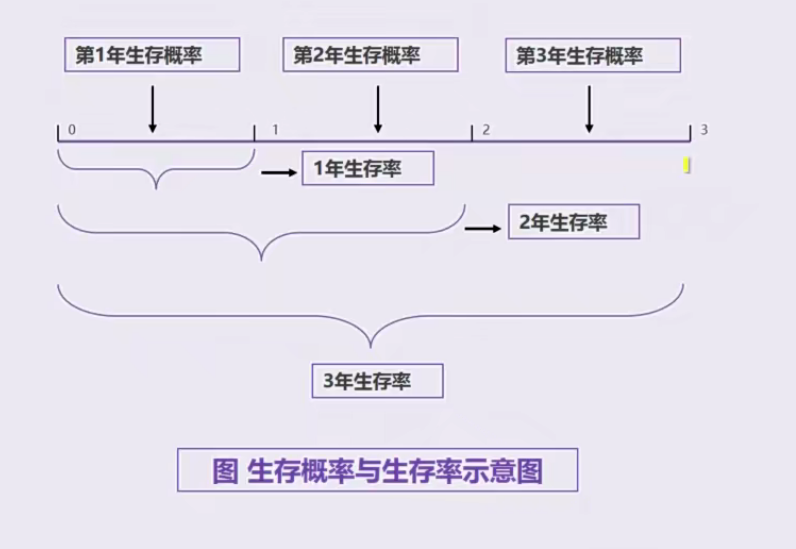
以构成比代替率
错误案例:
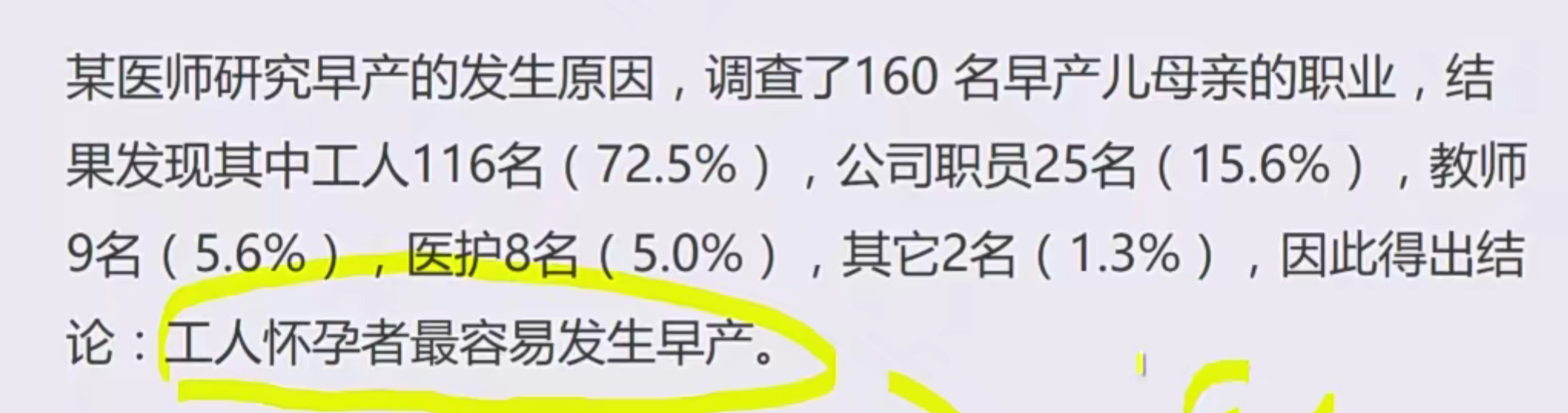
04.统计学方法选择与错误使用案例
误用类型1:误用普通卡方检验处理配对数据
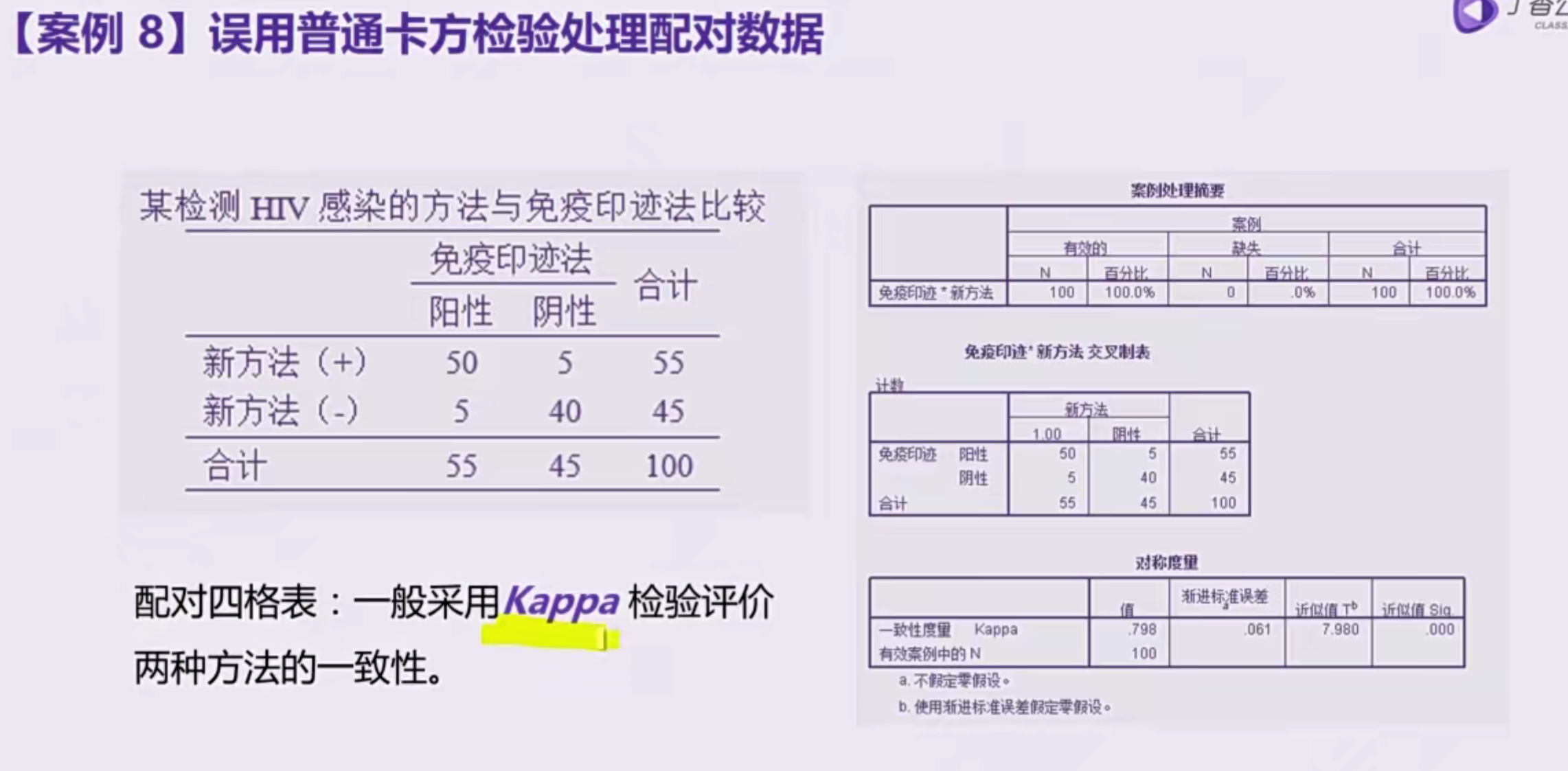
Kappa值取值-1~1,
Kappa值<0无实际意义
Kappa值>0.4一致性程度良
Kappa值>0.7一致性程度优
误用类型2:误用普通卡方检验处理等级资料(单向有序或双向有序)
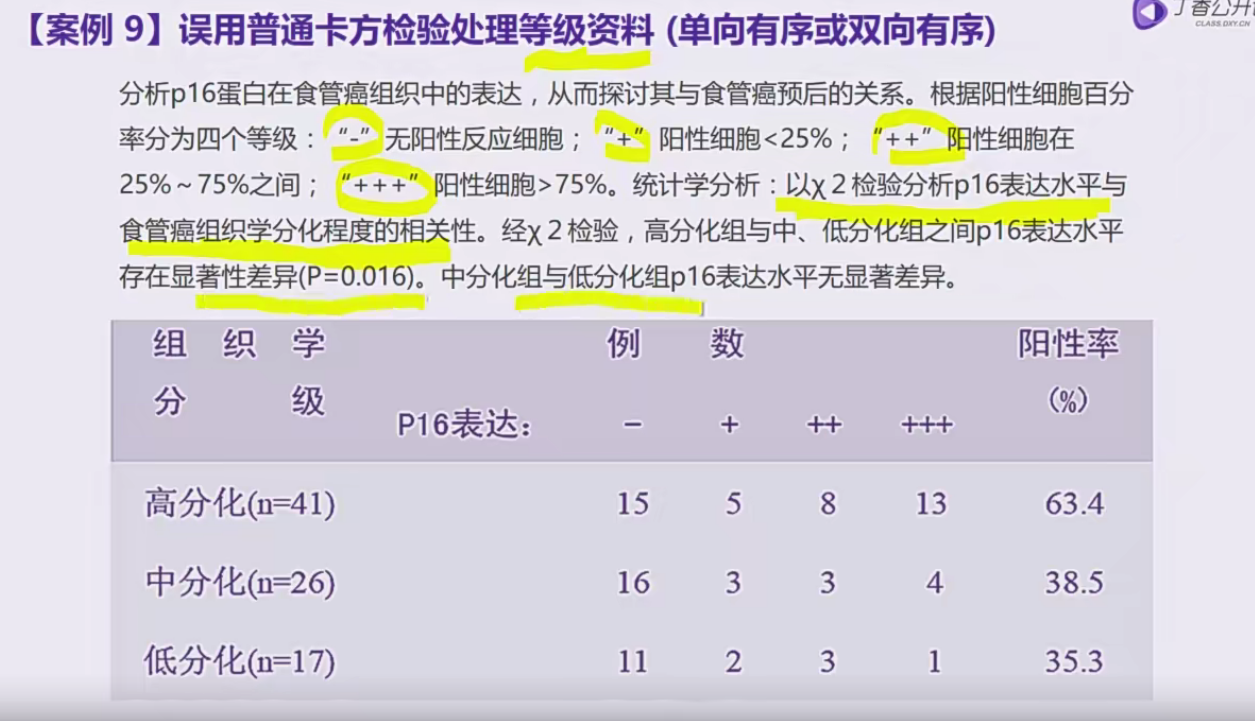
卡方检验在此处只能表示出P16表达构成比与组织学分级的相关性关系,并不能表示出表达率的关系
单向有序应当使用KWH分析,双向有序使用秩相关分析(spearman法)或双向有序资料的趋势性检验
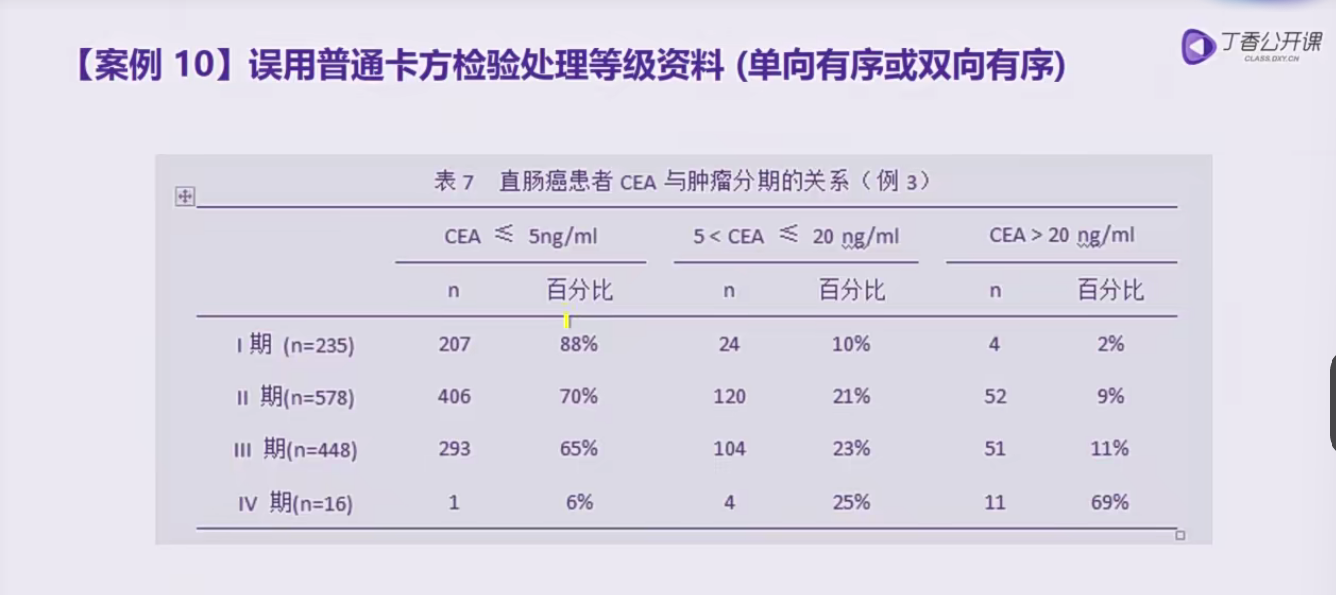
同理,若只把横纵变量当做分组变量,即只想得出构成比的相关性分析,可以使用普通卡方检验;若是单向有序应当使用KWH分析,双向有序使用秩相关分析(spearman法)或双向有序资料的趋势性检验
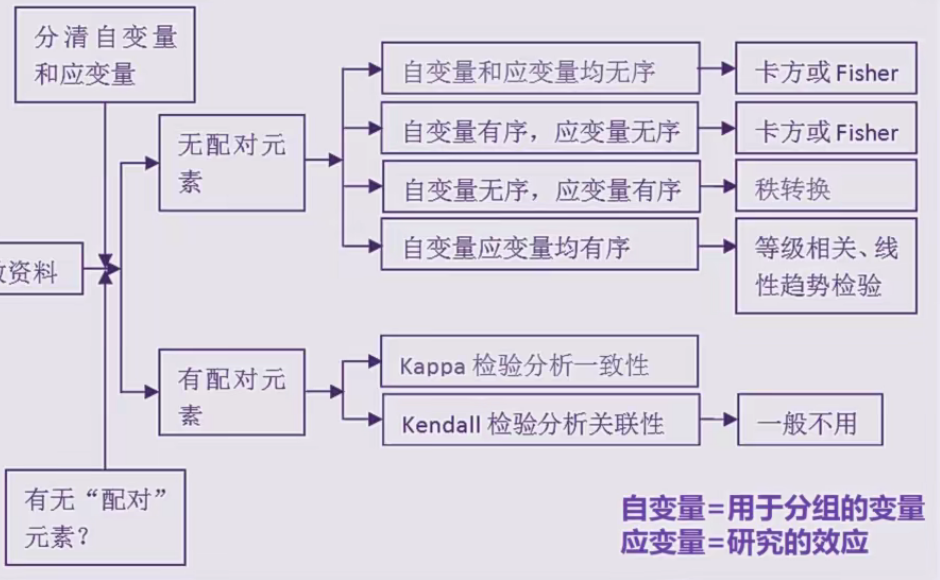
总结1:分类资料的一般处理原则
误用类型3:误用t检验处理偏态分布资料
独立样本t检验使用条件:正态分布、方差齐
两组偏态分布的连续变量比较一般采用MWU(Mann-Whitney U)秩和检验
误用类型4:误用独立样本t检验处理配对资料
两组配对资料的比较一般采用配对t检验或者配对Wilcoxon秩和检验
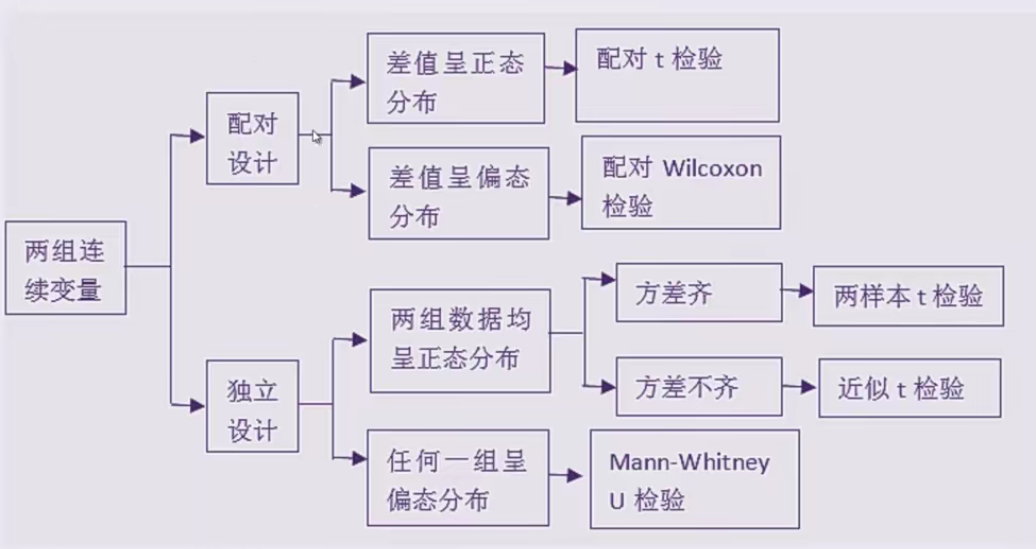
总结2:两组连续变量比较的统计学方法选择
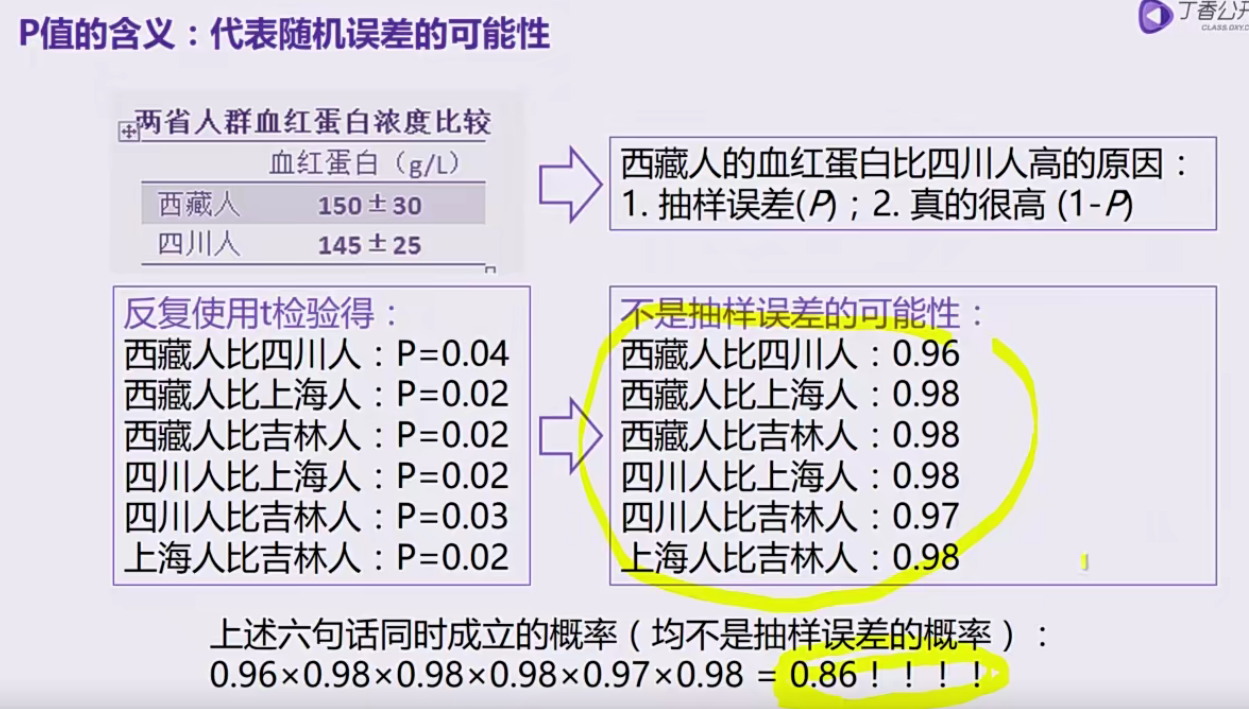
误用类型5:反复使用t检验处理多组资料比较
误用类型6:误用单因素方差分析处理偏态资料
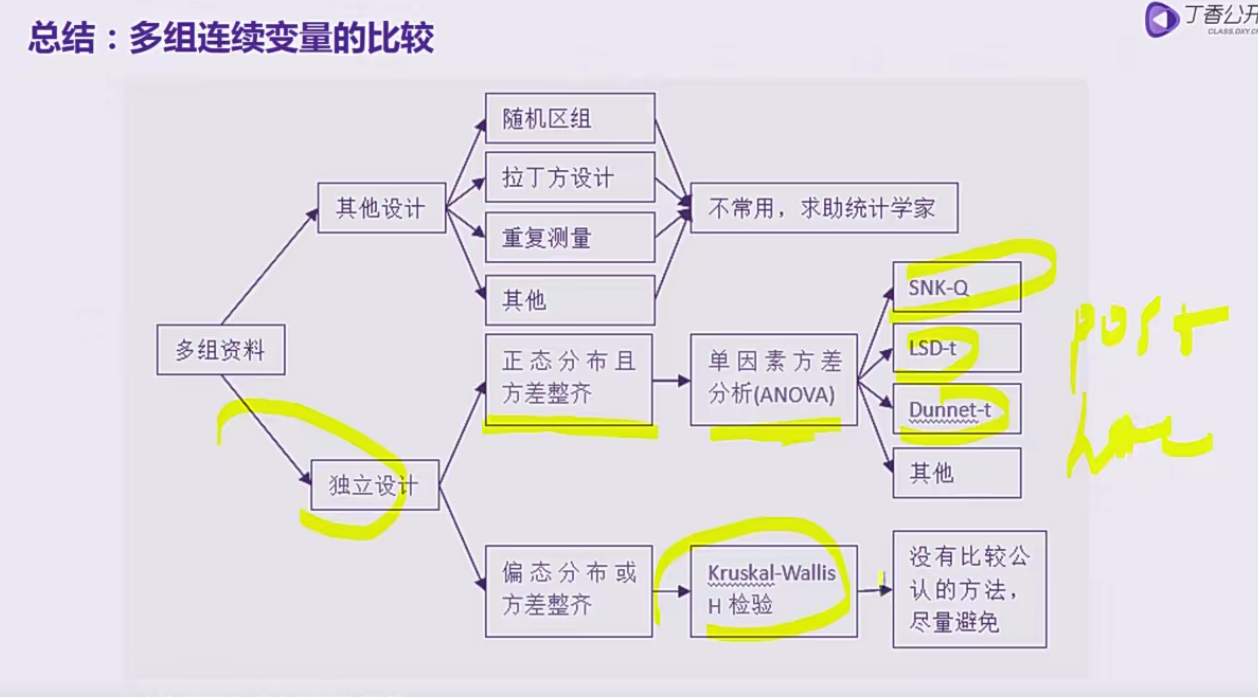
多组偏态资料的比较应采用KWH(Kruskal-Wallis H)检验
总结3:多组连续变量的比较
误用类型7:混淆Spearman相关与Pearson相关
两组均正态分布——Pearson相关
任意一组是偏态——Spearson相关
误用类型8:用时间点的生存率代替生存分析
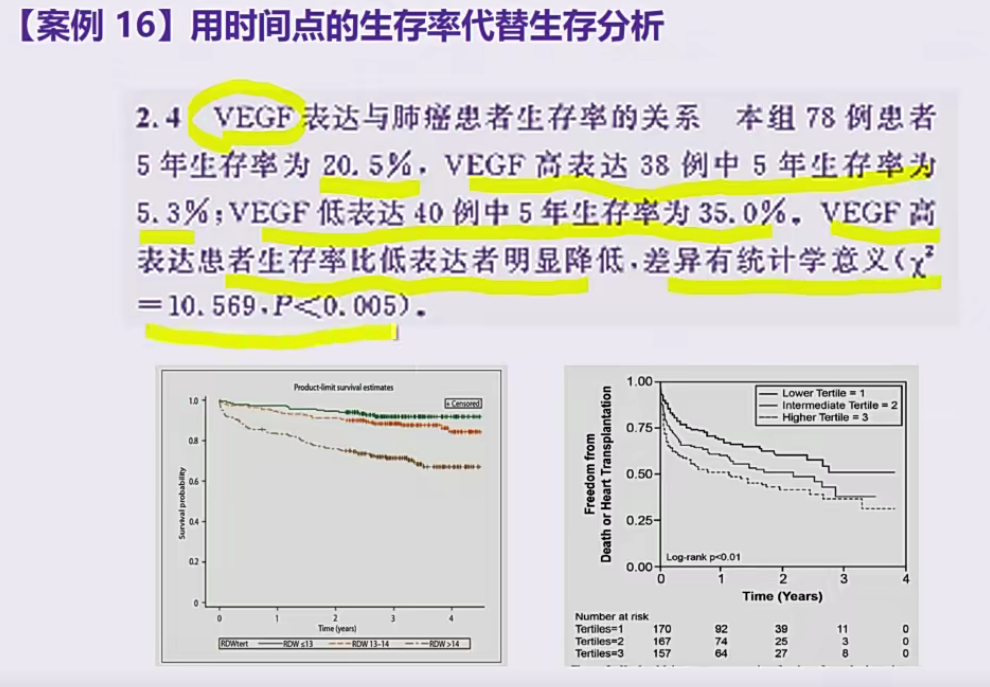
假设:VEGF高表达死亡均在第五年,VEGF低表达死亡均在第一年,那么此时统计学意义不大,所以卡方检验是显然错误的
应当使用图片下方两个图表的统计方法,KM(Kaplan Meier法)、logran、cox回归
误用类型9:多元线性回归的自变量多重共线性
误用类型10:缺乏校正混杂因素的统计学思维
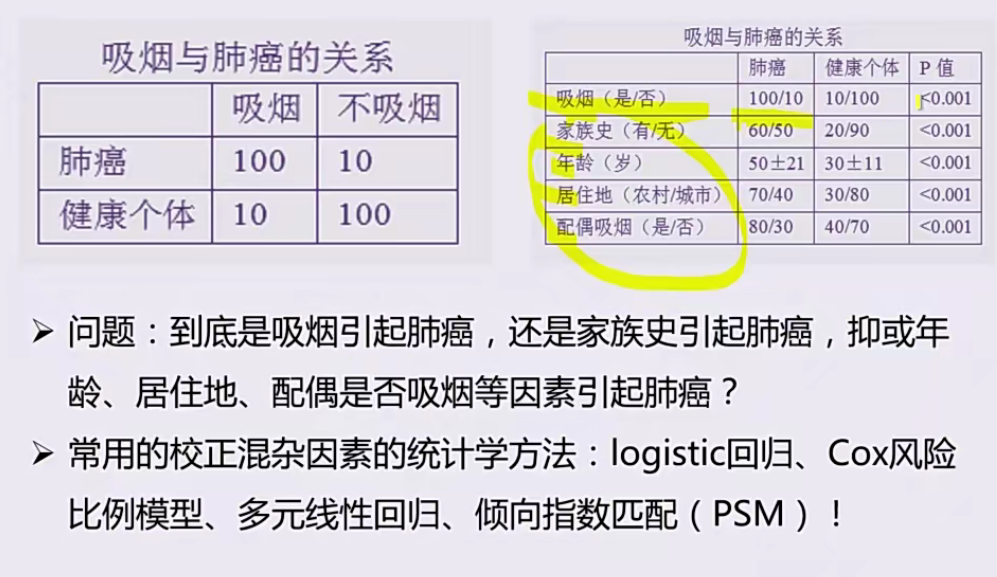
05:数据的类型与统计资料的描述
统计学概念
样本与总体
离散变量与连续变量
离散变量:计数值只能自然数和整数计算
连续变量:略
频率和概率
抽样误差与系统误差
系统误差:指在重复条件下对同一被测量进行无限多次测量所得结果的平均值与被测量真值之间的差值。它是由于实验设计的问题或者某些固定的原因引起的一类误差,具有重复性、单向性和可测性。系统误差可以通过校正的方法减少或者消除。在实验设计中,系统误差可以通过改进实验设计、使用标准物质或者校准仪器等方法来减小。
抽样误差:抽样方法本身所引起的误差,当用总体中随机的抽取样本时,哪个样本被抽到是随机的,但是所抽到的样本得到的样本指标与总体指标之间的偏差,比如说样本的均数与总体均数之间的偏差,实际上就是抽样误差造成的。抽样误差是不可避免的,但是当样本足够大的时候,它一般会变小。
变异与同质
变异:变异是指样本或总体内每个个体之间的差异,反映了个体之间的变化和分散程度。变异越大,说明个体之间的差异越大,数据的分布越广。
同质:是指样本或总体内每个个体之间的相似性和一致性。如果样本内每个个体之间的数据都很接近,说明同质性较高,数据的分布较为集中。
均数与中位数
均数:反映正态分布集中趋势
中位数:反映偏态分布的集中趋势
标准差与四分位数间距
都是反映数据的离散趋势
标准差反映正态分布
四分位数间距一般反映偏态分布
方差与标准差
也是反映数据的离散趋势
标准误与可信区间
标准误与可信区间是统计学中用于评估样本数据可靠性和预测总体参数的方法。
标准误(Standard Error)是样本均数标准差的估计值,用于衡量样本均数的抽样误差。标准误越小,样本均数的抽样误差越小,样本均数的代表性越高。
可信区间(Confidence Interval)是指根据样本数据估计总体参数的可能范围。可信区间的大小取决于样本大小和标准差,样本越大,标准差越小,可信区间越窄,表示对总体参数的估计越准确。
数据类型
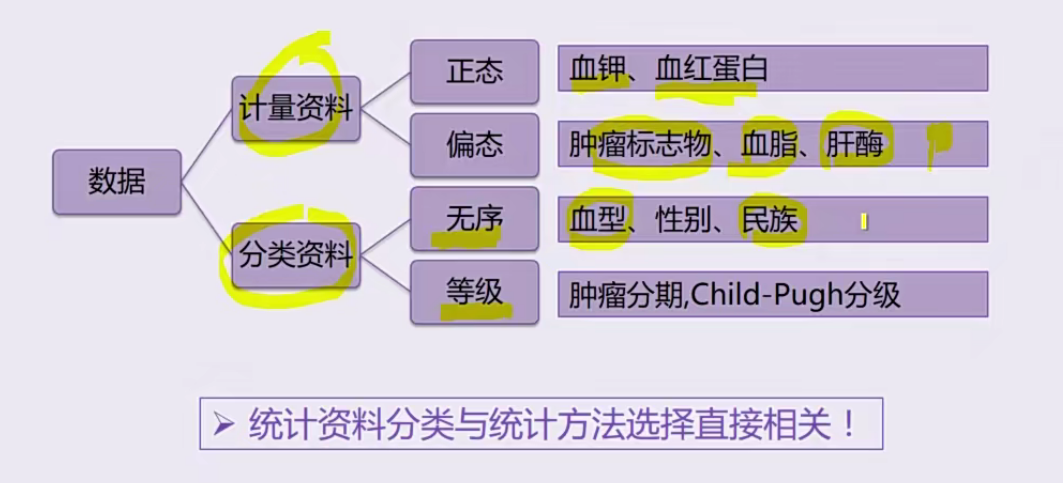
计量资料
简单成组设计的统计学方法选择(计量资料)

方差分析的类型(计量资料)

复杂成组设计的统计学方法选择(计量资料)

相关分析(计量资料)
线性相关
适用于二元正态分布的统计资料,常用Pearson相关系数表示
秩相关
总计分布未知或等级资料等不符合双变量正态分布,用Spearson
因果联系(计量资料)
简单线性回归
因变量为连续变量,自变量仅1个
多重线性回归
因变量为连续变量,自变量多个
分类变量
四格表统计方法选择(分类资料)

列联表统计方法选择(分类资料)
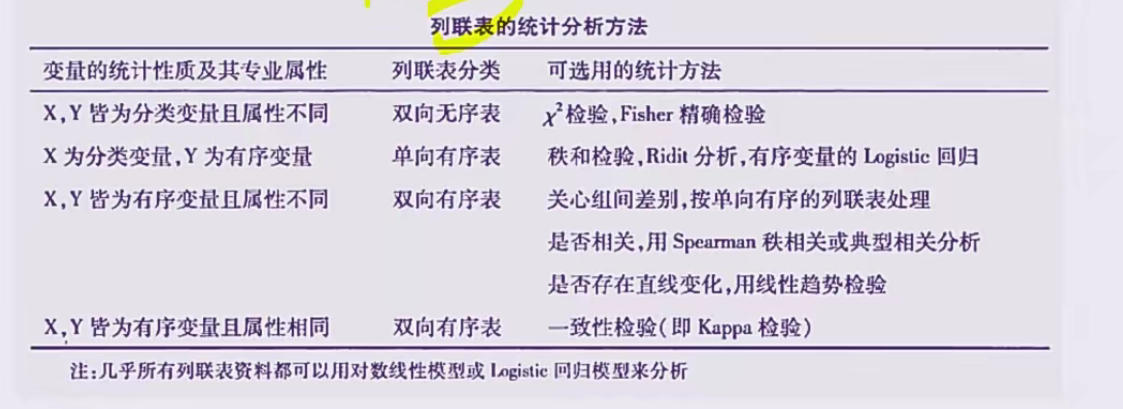
因果联系(分类资料)
非条件logistic回归——非配对设计
条件logistic回归——配对设计
三大回归

医学统计学学习笔记2
06 两组连续性资料的比较
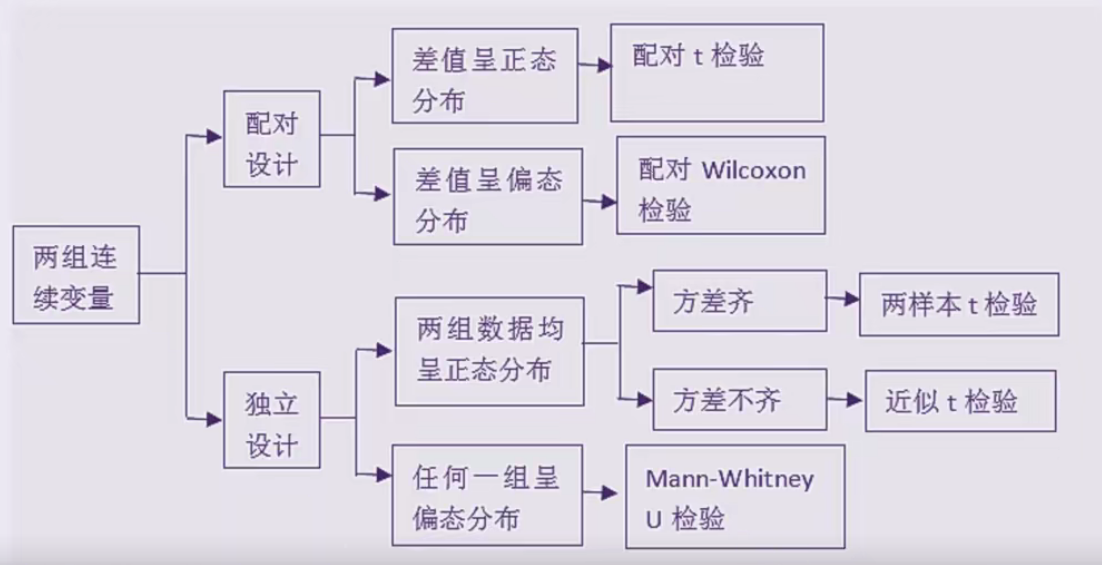
SPSS操作(暂不做要求)
- 如何定义数据
- 如何录入数据
- 如何从外部导入数据
- 一些基本操作
t检验
适用条件
- 随机样本,即数据满足独立性
- 各样本代表的总体符合正态分布
- 各样本代表的总体方差齐
单样本t检验
单样本t检验是用来确定样本均值是否与已知或假设的总体均值上再统计上有显著不同
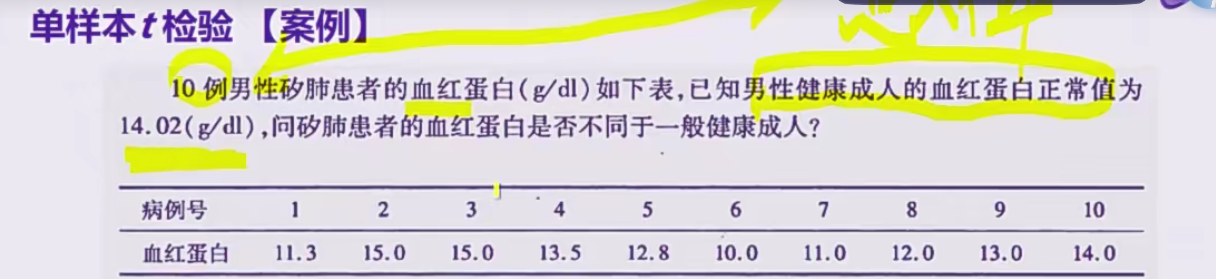
男性健康成人的血红蛋白正常值——总体
矽肺患者的血红蛋白值——样本
算出p值小于0.05则具有统计学意义
配对t检验
它是指在不同条件下,对同一个整体获取的样本进行分析,以评价条件对其的影响,其中包括不同存放环境、不同测量系统等
将两种同类对象按不同方式分类,比如:
- 对同一科目进行前后对比观察;
- 对同一测试者,比较两种不同测量方法或两种不同处理方法的区别

算出p值小于0.05则具有统计学意义,即干预有效
成组t检验(完全随机设计的t检验,两独立样本的t检验)
评价条件对其的影响

若方差齐则正常读取,方差不齐则进行校正t检验
秩和检验
- 不符合正态分布
单样本秩和检验

配对样本秩和检验
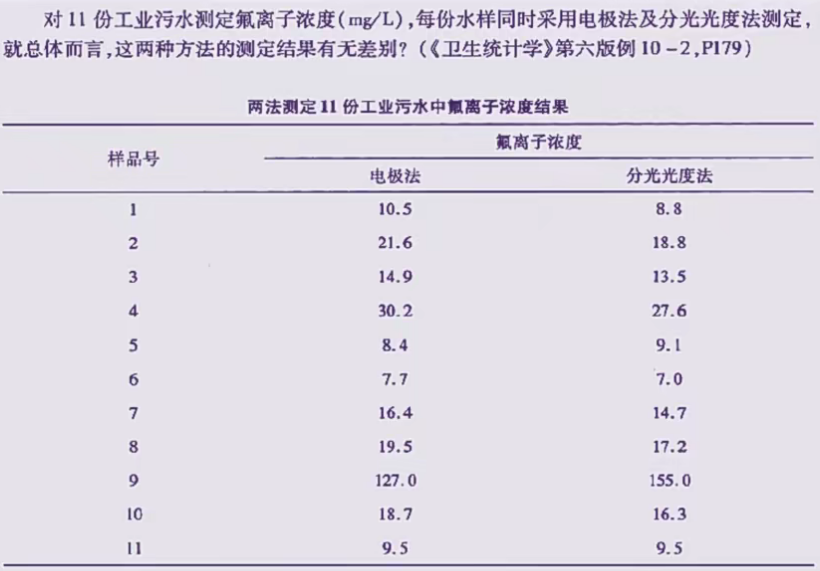
两组独立样本秩和检验
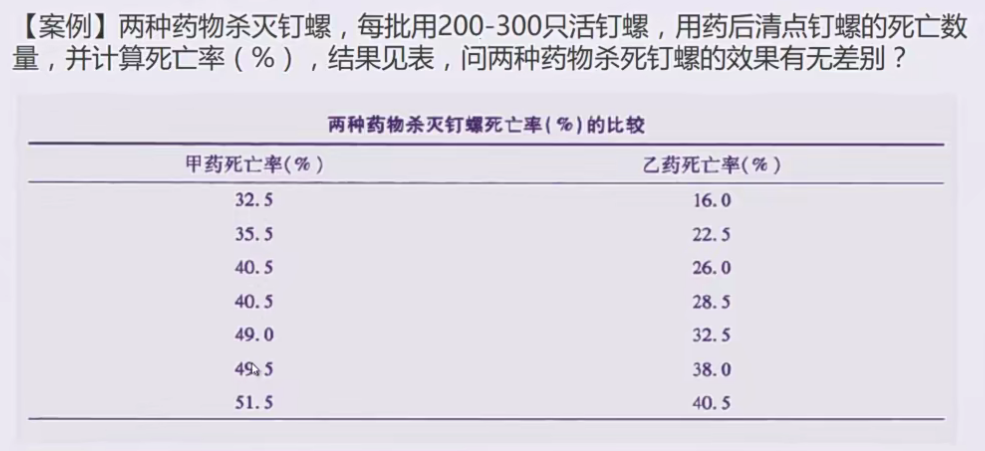
07 多组连续型变量比较(单因素)
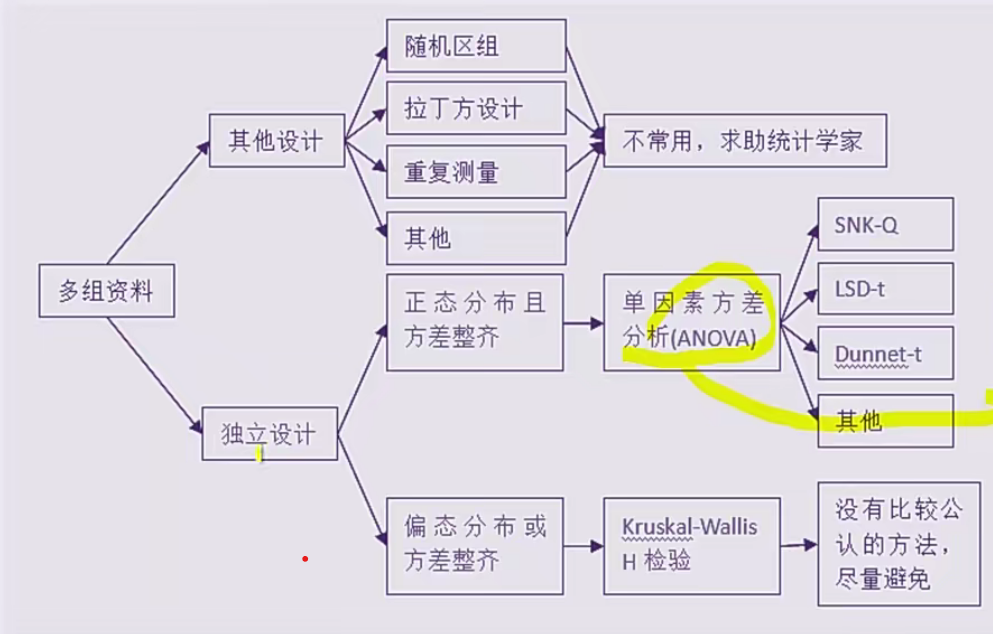
单因素方差分析(one-way anova)
试验中要考察的指标称为试验指标,影响试验指标的条件称为因素,因素所处的状态称为水平,若试验中只有一个因素改变则称为单因素试验,若有两个因素改变则称为双因素试验,若有多个因素改变则称为多因素试验。方差分析就是对试验数据进行分析,检验方差相等的多个正态总体均值是否相等,进而判断各因素对试验指标的影响是否显著,根据影响试验指标条件的个数可以区分为单因素方差分析、双因素方差分析、多因素方差分析
适用条件:
- 各组独立设计
- 样本所代表的总体正态分布
- 样本所代表的总体方差整齐
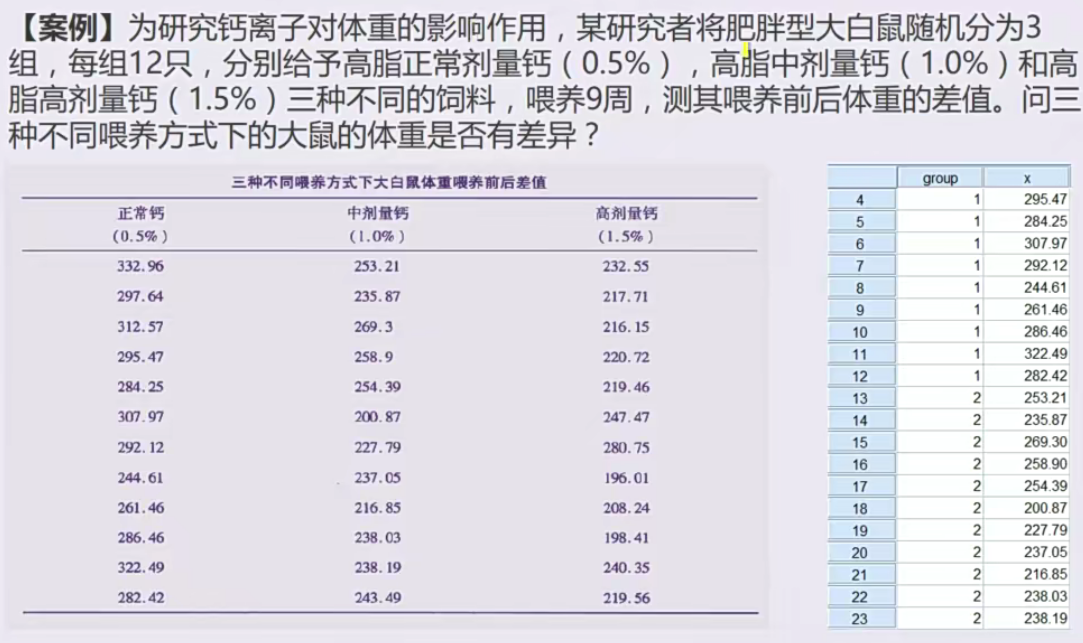
单因素——喂养方式
因变量(Dependent List):体重改变值(连续型变量)
分析表格
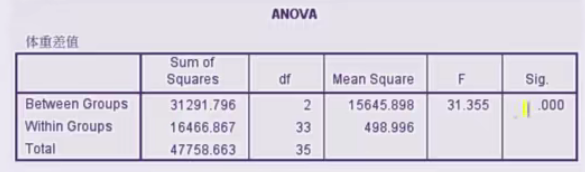
方差(variance):方差是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。
- 组间差异(Between Groups)
- 组内差异(Within Groups)
- 均方(Mean Square):衡量组间差异大小,组内差异大小,由离均差平方和除以样本量得出
- 离均差平方和(Sum of Squares):
- 自由度(degree of freedom,df):
- F值(显著性差异水平):组间差异均方/组内差异均方得出,F越大,说明组间差异越大越显著
- P值(Sig):代表显著性检验的结果,用于判断观察到的统计结果与预期结果的差异是否具有统计学意义。通常0.01<p≤0.05被认为具有统计学意义,而0.001≤p<0.01被认为具有高度统计学意义
组间比较
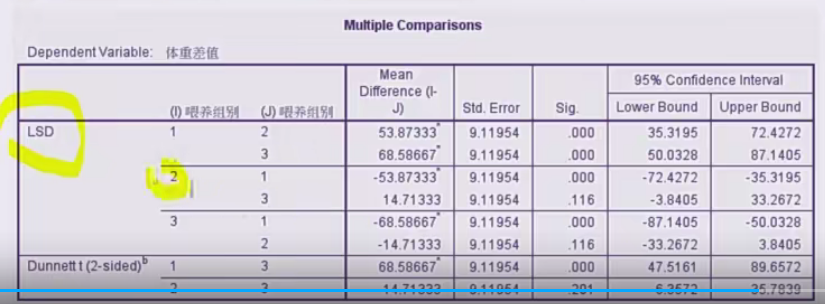
08 多组连续型变量比较(双因素、重复测量)
两因素方差分析(two way anova)
随机区组设计的方差分析
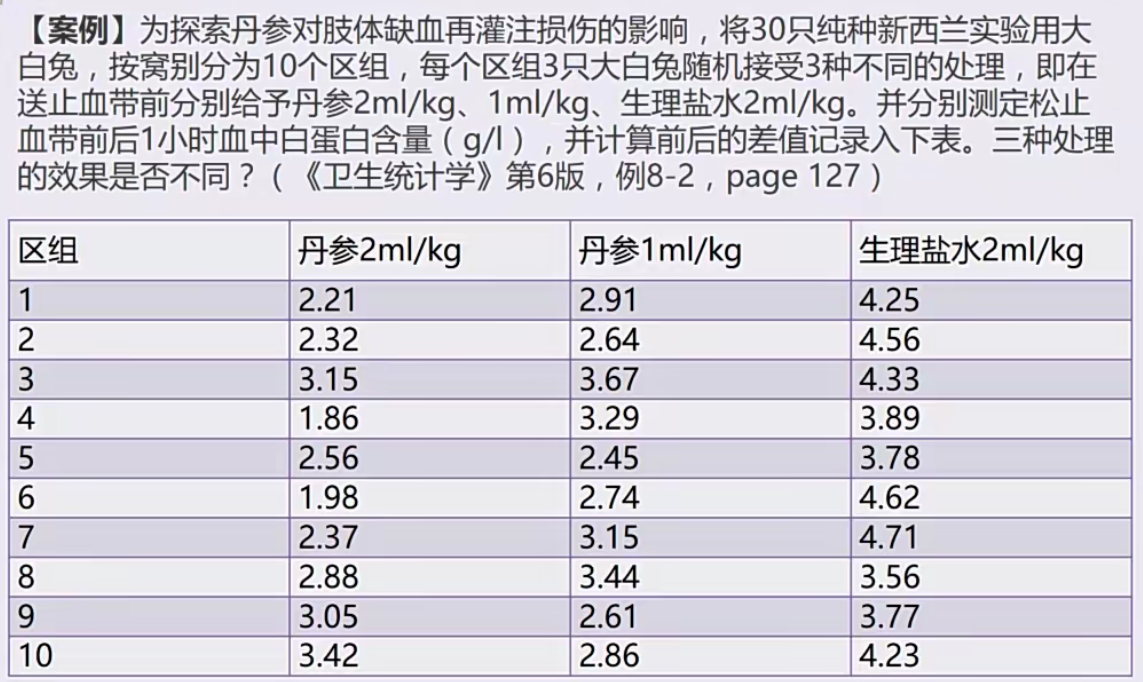
实验因素:丹参剂量,3个水平
非实验因素:窝别,10个水平
因变量:血中白蛋白含量变化值
析因设计资料方差分析
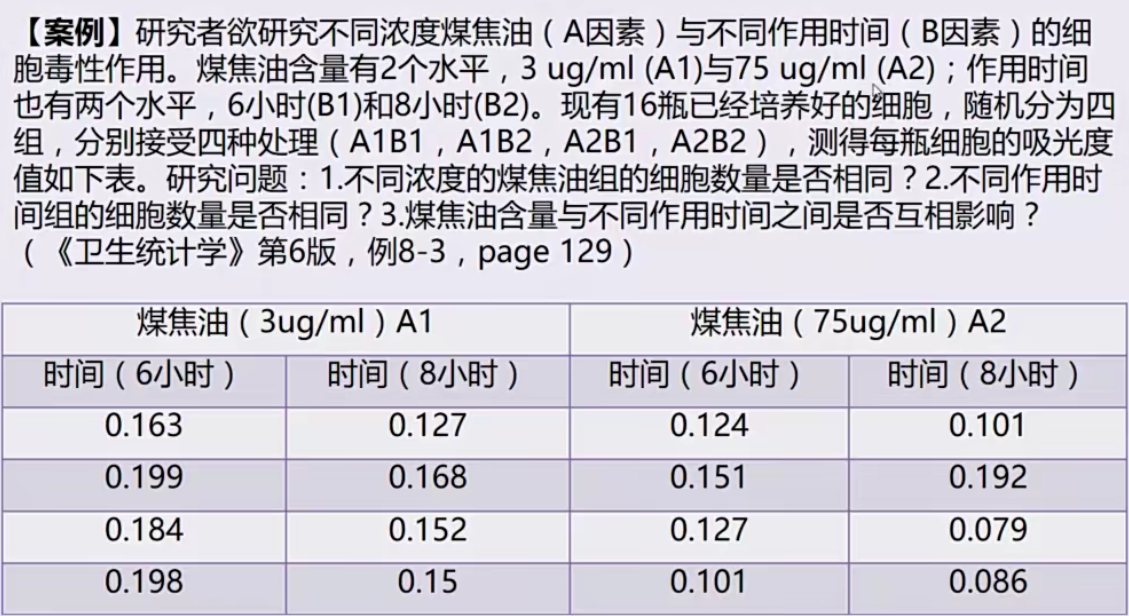
两个因素都为实验因素,需要探究两个因素的交互性
因变量:吸光度值
分析表格
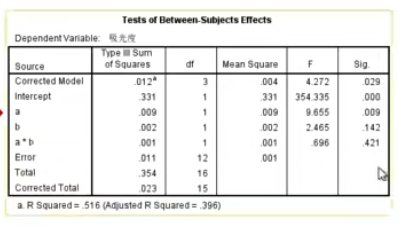
因为a*b的sig=0.421,即两个因素并没有交互,所以两个因素并没有相互影响
因为a的sig=0.009,所以药物浓度对细胞数量有差别,具有统计学意义
又因为b的sig=0.142,所以不同药物作用时间对细胞数量的差别不具有统计学意义

重复测量资料的方差分析
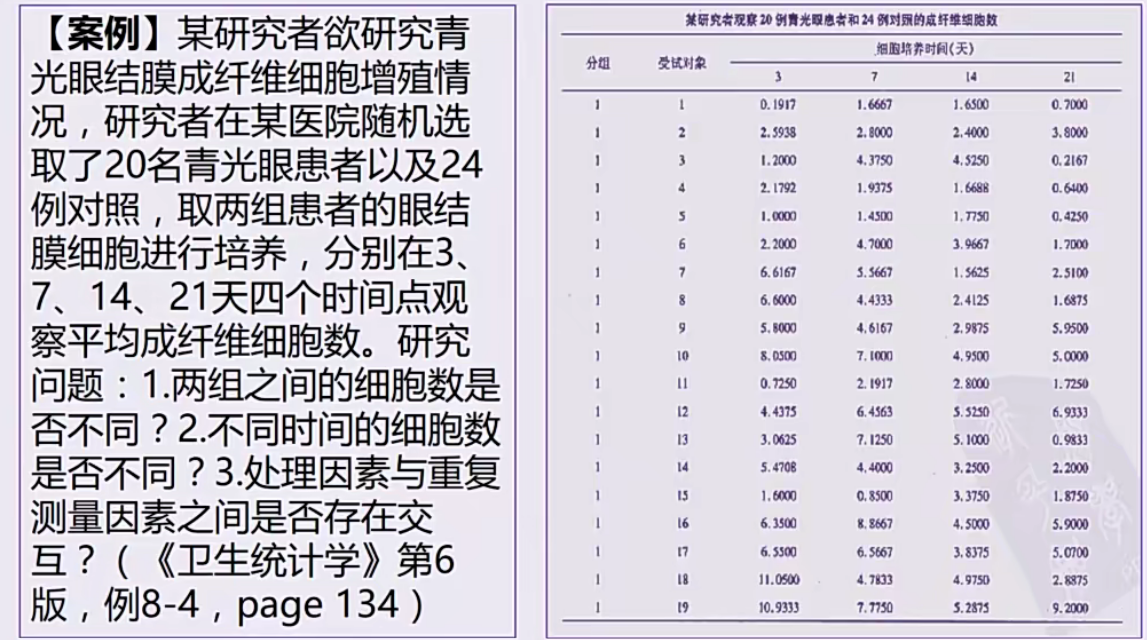
后一时间点的测量结果受前一时间点测量结果影响
一般的双因素方差分析是指无交互作用的两个因素的方差分析.
重复双因素方差分析是指重复测量因素具有交互作用的方差分析.
表格分析
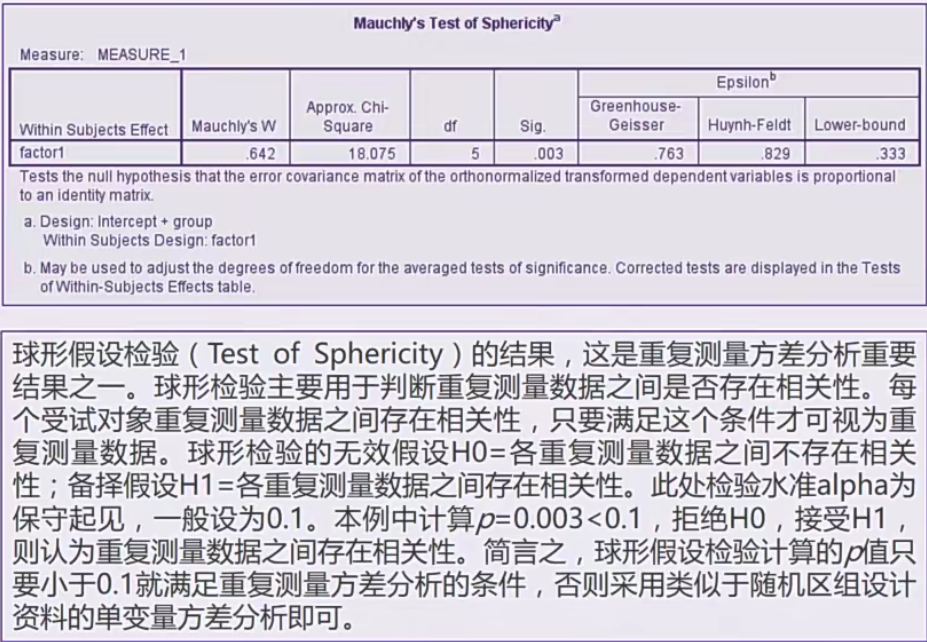
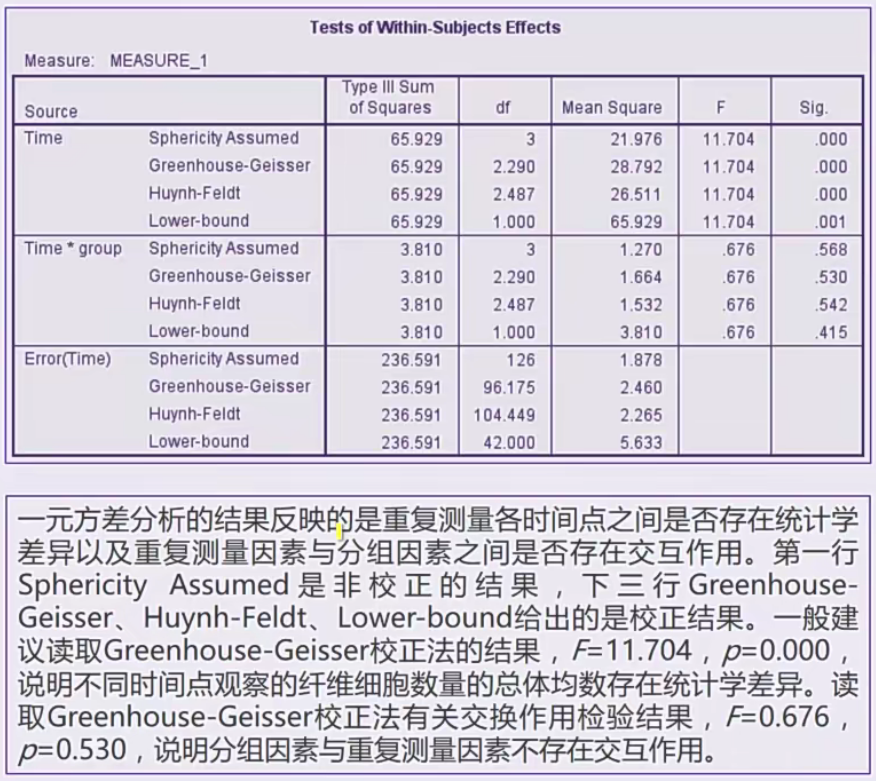
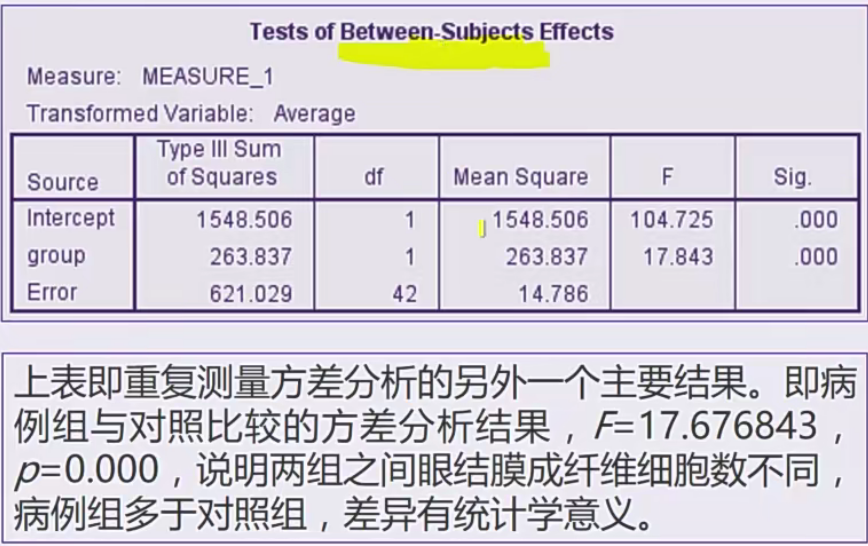
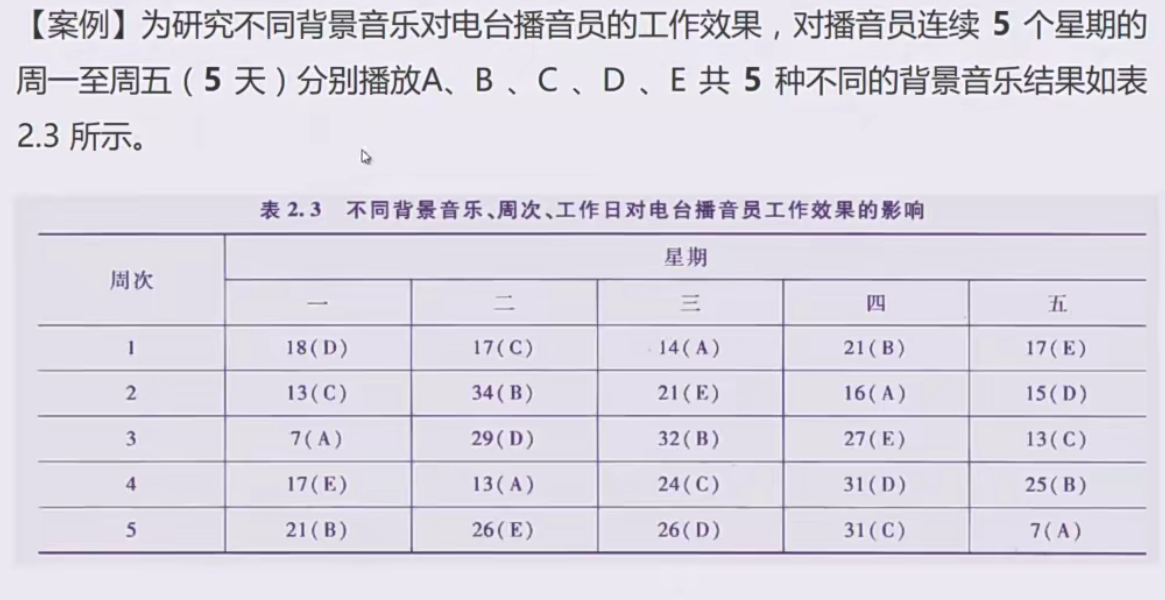
拉丁方设计方差分析——two way anova
简单理解:是析因设计的扩展版,只不过拉丁方设计不考虑交互
特征:每个因素的水平数相等(一般不超过8)
完全随机设计只涉及一个处理因素,但随机区组设计涉及一个处理因素,一个区组因素(或称为配伍因素);倘若实验研究涉及一个处理因素和两个控制因素,每个因素的类别数或者水平数相等,那么此时可采用拉丁方设计来安排实验。
协方差分析
协方差分析(analysis of covariance, ANCOVA)
适用条件:
- 残差独立
- 符合正态分布
- 方差齐
- 各处理之间应变量对协变量的回归系数差别无统计学意义
案例

分组变量:教学方法
结果变量:期末成绩
基线,协变量:摸底成绩
不考虑摸底考试成绩,对教学方法与期末成绩进行t检验即可
使用协方差分析,需要先检验协变量和分组变量有无交互,无交互才可进行协方差分析
本质上协方差设计就是线性模型,这个案例也可以使用多元线性回归来解决(后面会讲)
09 多组连续型变量比较(秩和检验)
秩和检验
秩和检验(rank sum test)又称顺序和检验,它是一种非参数检验(nonparametric test)。它不依赖于总体分布的具体形式,应用时可以不考虑被研究对象为何种分布以及分布是否已知,因而实用性较强。
主要用于比较多个样本或者观测值之间的秩次(也称为等级)是否有显著差异
配对
对配对比较的资料应采用符号秩和检验(signed-rank test),其基本思想是:若检验假设成立,则差值的总体分布应是对称的,故正负秩和相差不应悬殊。检验的基本步骤为:
(1)建立假设;
H0:差值的总体中位数为0;
H1:差值的总体中位数不为0;检验水准为0.05。
(2)算出各对值的代数差;
(3)根据差值的绝对值大小编秩;
(4)将秩次冠以正负号,计算正、负秩和;
(5)用不为“0”的对子数n及T(任取T+或T-)查检验界值表得到P值作出判断。
应注意的是当n>25时,可用正态近似法计算u值进行u检验,当相同秩次较多时u值需进行校正。
成组
两样本成组资料的比较应用Wilcoxon秩和检验,其基本思想是:若检验假设成立,则两组的秩和不应相差太大。其基本步骤是:
(1)建立假设;
H0:比较两组的总体分布相同;
H1:比较两组的总体分布位置不同;检验水准为0.05。
(2)两组混合编秩;
(3)求样本数最小组的秩和作为检验统计量T;
(4)以样本含量较小组的个体数n1、两组样本含量之差n2-n1及T值查检验界值表;
(5)根据P值作出统计结论。
同样应注意的是,当样本含量较大时,应用正态近似法作u检验;当相同秩次较多时,应用校正公式计算u值。
多样
多个样本比较的秩和检验可用Kruskal-Wallis法,其基本步骤为:
(1)建立假设;
H0:比较各组总体分布相同;
H1:比较各组总体分布位置不同或不全相同;检验水准为0.05。
(2)多组混合编秩;
(3)计算各组秩和Ri;
(4)利用Ri计算出检验统计量H;
(5)查H界值表或利用卡方值确定概率大小。
应注意的是当相同秩次较多时,应计算校正Hc
等级
这类资料的特点是无原始值,只知其所在组段,故应用该组段秩次的平均值作为其秩次,在此基础上计算秩和并进行假设检验,其步骤与两组或多组比较秩和检验相同。需注意的是由于样本含量较多,相同秩次也较多,应用校正后的u值和H值。
多组独立样本的秩和检验(Kruskal-Wallis H)
用于推断计量资料或等级资料的多个独立样本所来自的多个总体分布是否有差别
案例1

此案例采用生存分析最合适,但是因为样本量太少所以效果不理想,故采用秩和检验
案例2
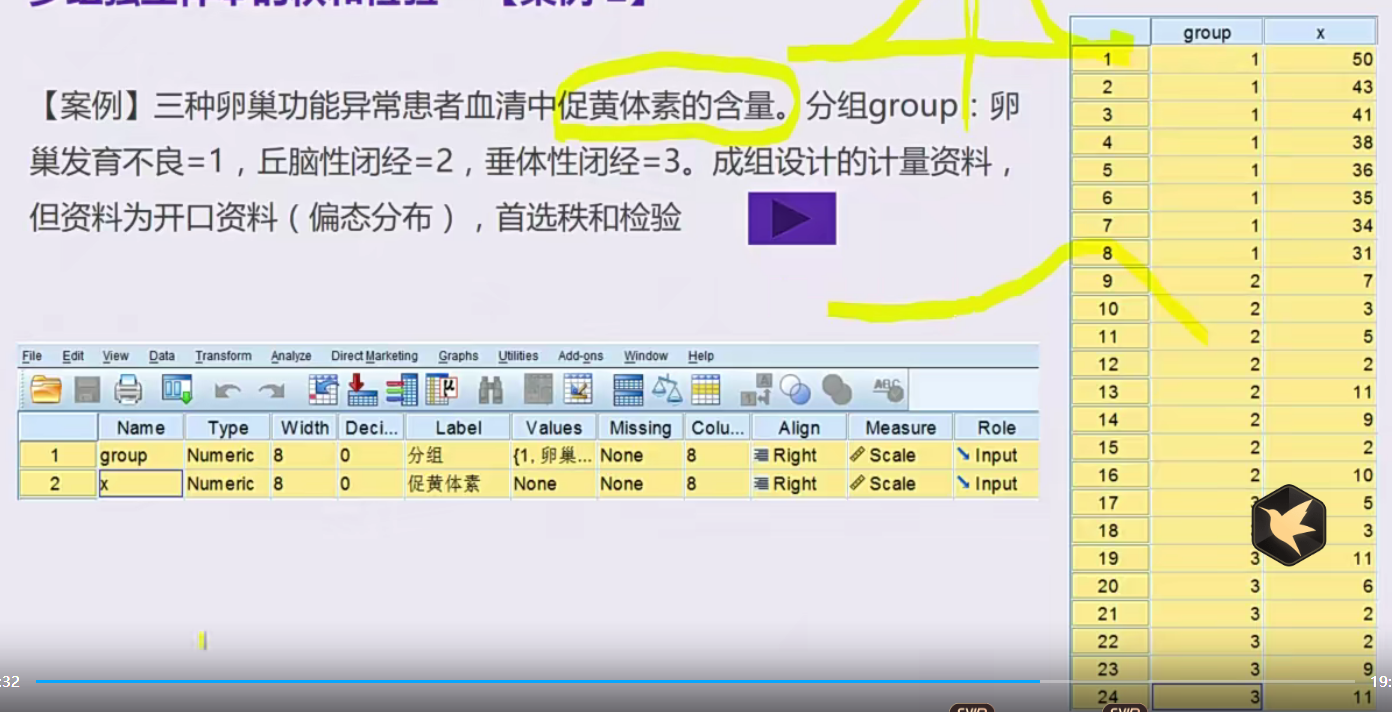
10 分类资料的统计学处理
统计方法的选择

普通卡方检验
卡方检验(chi-square test)
卡方检验可以用于推断两个总体率之间有无差别,多个总体率之间有无差别,多个样本率间多重比较,两个分类变量之间有无关联性和频数分布拟合优度。
使用普通卡方检验的条件
- 样本量大于等于40
- 最小的理论频数(期望值)不小于5,若小于5则读取/使用连续性校正的卡方检验
- 没有单元格的理论频数小于1,若小于1则读取/使用Fisher‘s 精确概率法
- 满足以上条件即可读取Pearson卡方
案例(四格表资料的卡方检验)
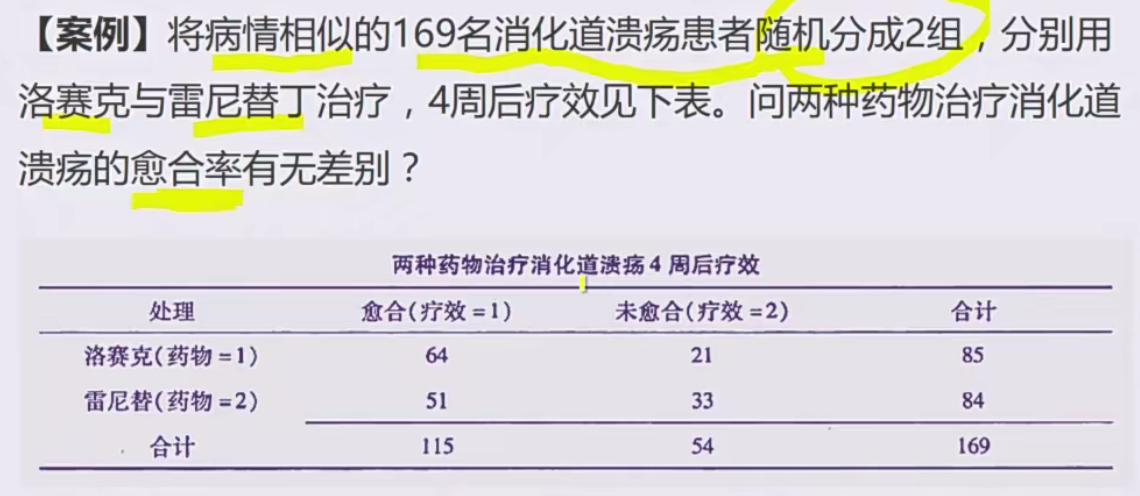
和高中卡方检验一样……(一开始还没看出来笑死)
11 配对卡方检验与一致性检验
例子1
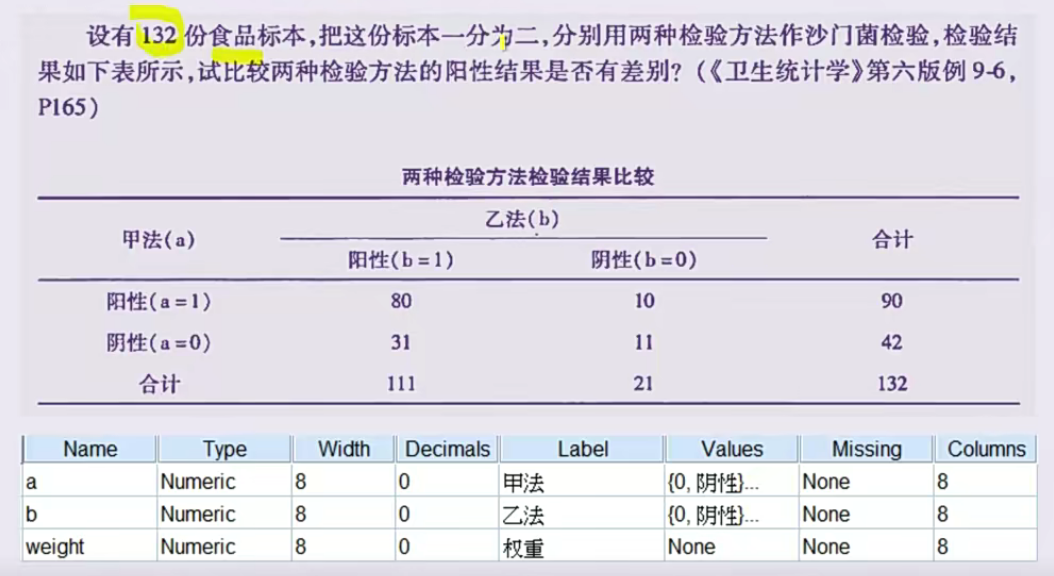
例子结果分析

配对四格表与普通四格表的区别
- 普通四格表适用于根据不同的实验条件分类得到不同实验结果的资料,例如根据是否吸烟分组得到是否患癌症的人数。
- 配对四格表适用于先将实验对象配对后随机安排到两个不同处理组,所得的二分类结果的资料。例如,同一批对象两个时间点(或两个部位)的测定,或同一对象用两种方法(或两种仪器、两名化验员、两种条件)的测定,所得的二分类(如阳性、阴性)结果的资料
例子2
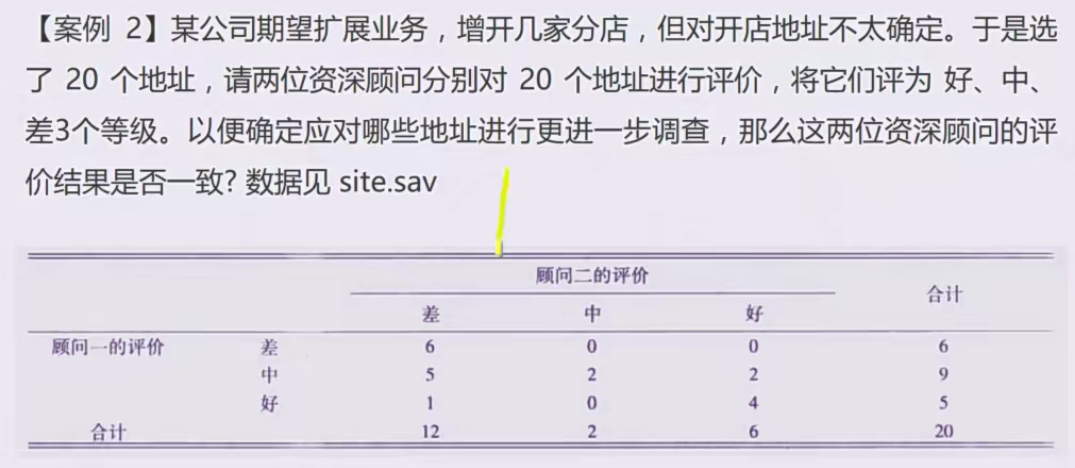
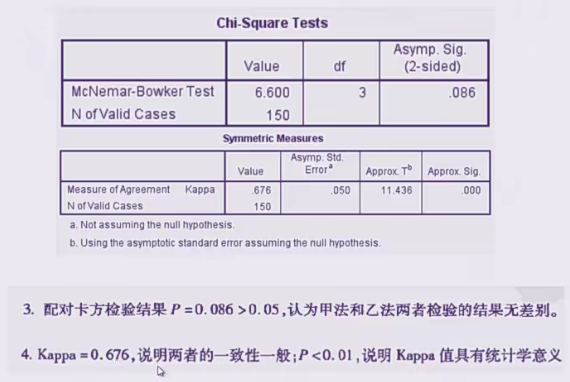
结果分析
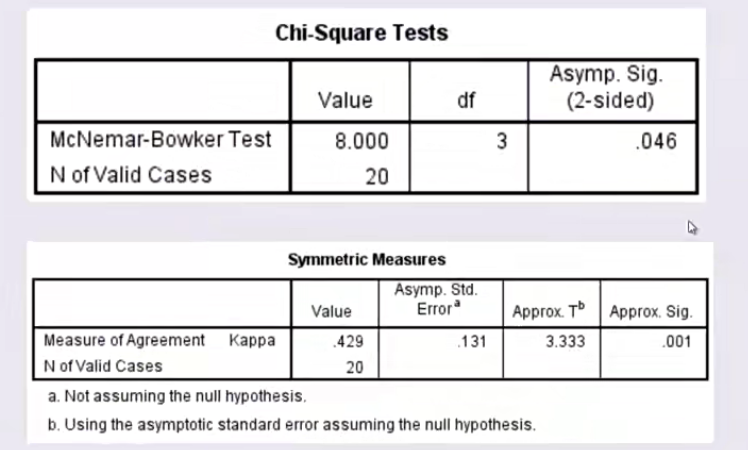
可以发现配对卡方的P(sig)值<0.05,认为两个甲乙顾问好评率的差异具有统计学意义,而下面的图中检验出的Kappa值为0.429>0.4,说明具有中等一致性程度,且sig为0.001<0.05说明kappa值具有统计学意义

12 列联表(行×列表)分析——单项有序
接下来的一段文字与本节内容基本无关,只是作为一个小拓展
行×列表资料的分析主要用于多个样品率的比较、两个或多个构成比的比较以及双向无序分类资料的关联性检验。主要有以下三种情况
- 多个样品率比较时,有R行2列,称为R×2表
- 两个样本的构成比比较时,有2行C列,称为2×C表
- 多个样本的构成比比较以及双向无序分类资料关联性检验时,有R行C列,称为R×C表
单项有序:结果变量有序,即结果变量为等级资料
例子1(单项有序)
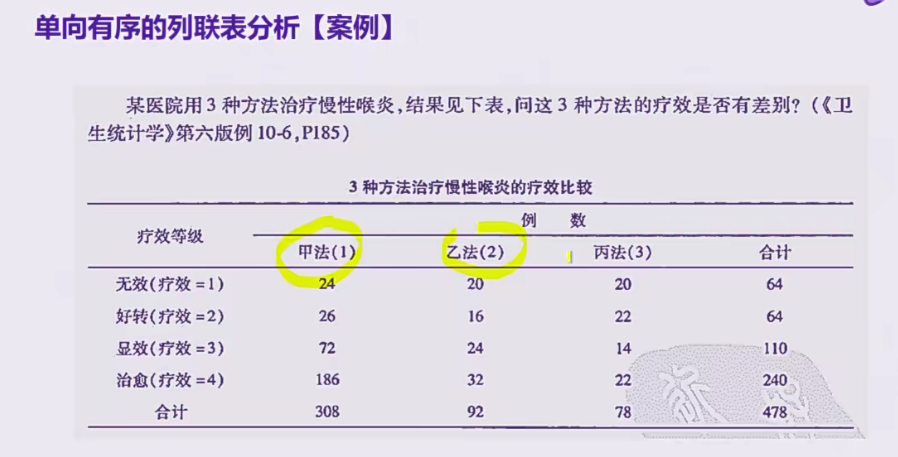
结果变量:疗效(等级资料)
使用Kruskal-Wallis分析
回顾Kruskal-Wallis分析:用于推断计量资料或等级资料的多个独立样本所来自的多个总体分布是否有差别
例子2(双向无序)
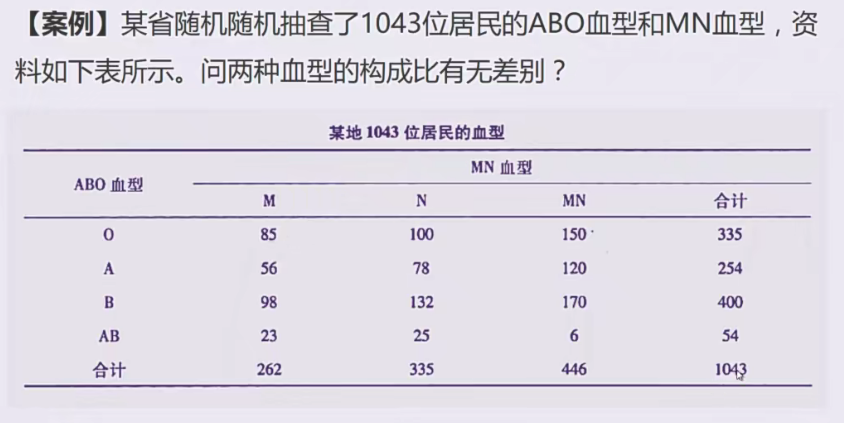
使用普通卡方检验即可
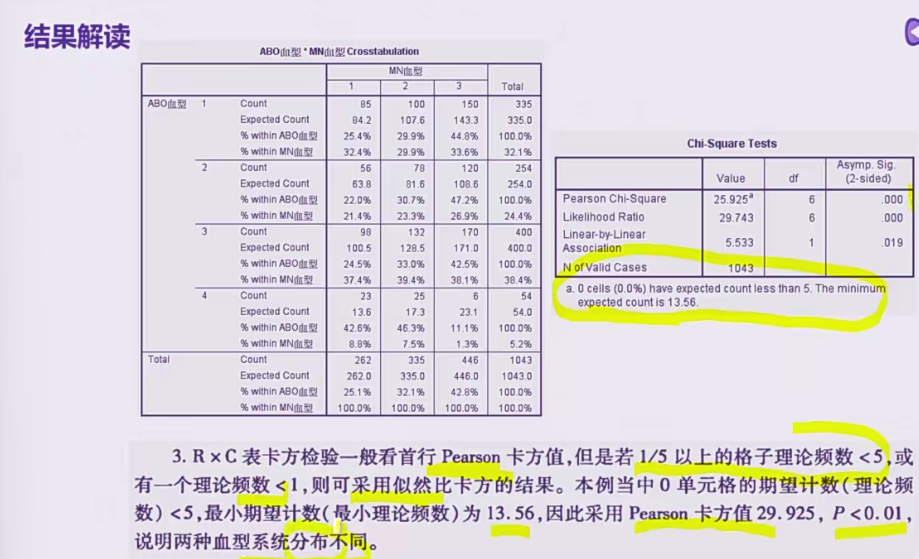
13 双向有序列联表的统计学处理
例子1:双向有序且属性不同
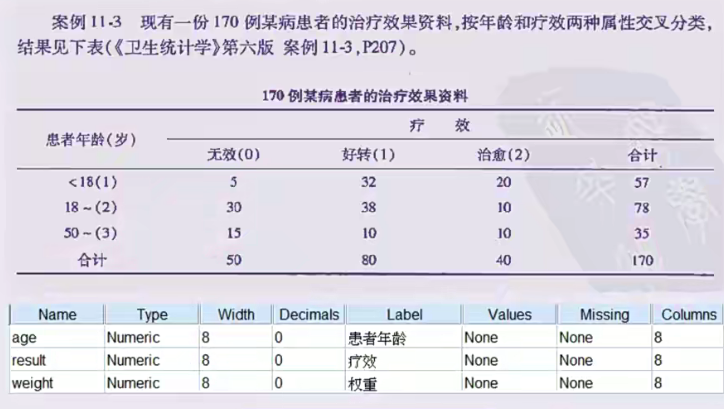
- 若关心组间(不同年龄)差别则使用秩和检验
- 若关心两变量是否相关则使用sperman秩相关
结果分析
秩和检验:

spearman秩相关:
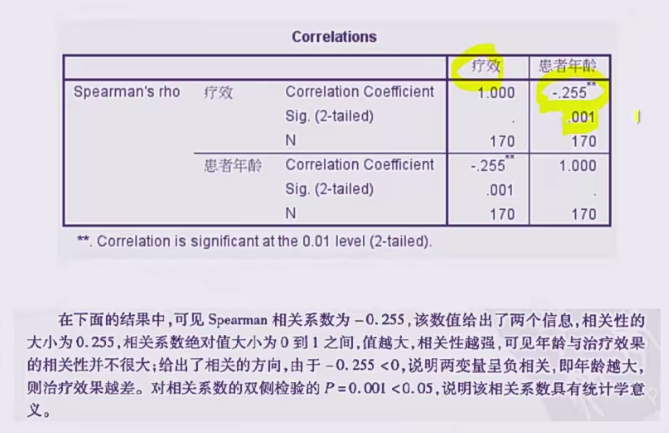
例子2:双向有序且属性相同
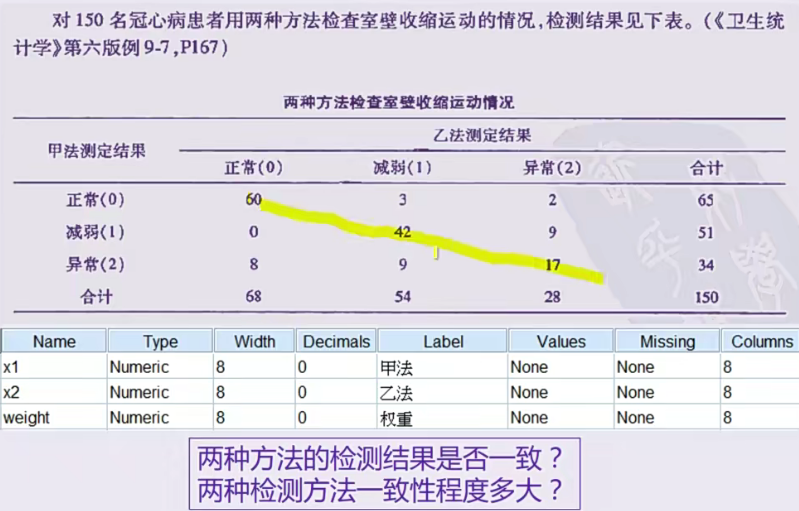
结果分析
14 诊断试验设计要点以及统计学指标的含义
设计方法
诊断实验的设计方法主要有三种:
- 队列研究设计:这是最好的设计方法,通常是一种前瞻性的研究。在这种设计中,一组人被随机分为两组,一组接受A诊断方法,另一组接受B诊断方法。这种方法主要用于筛查实验或有创新的检查手段。
- 横断面设计:这是最常用的设计方法。例如,对于一组高度怀疑有肺癌的人,他们都会先进行CT检查,然后再进行穿刺活检。活检的结果是精标准的检查结果,与CT的结果进行比较。这种方法可以评估诊断方法的准确度。
- 病例对照设计:这是最差的设计方法,虽然易于开展,但偏移较大。例如,如果纳入的研究病例过于严重,可能会高估诊断方法的准确度;如果纳入的病例病情较轻,可能会低估诊断方法的准确度。在选择诊断实验的设计方法时,需要根据具体的研究目的、资源、伦理等因素进行综合考虑。
统计学指标
诊断试验的统计指标基本概念重点包括敏感度、特异度、ROC曲线分析和凹透镜线(LC曲线)。这些指标用于评估诊断试验的准确性和可靠性。
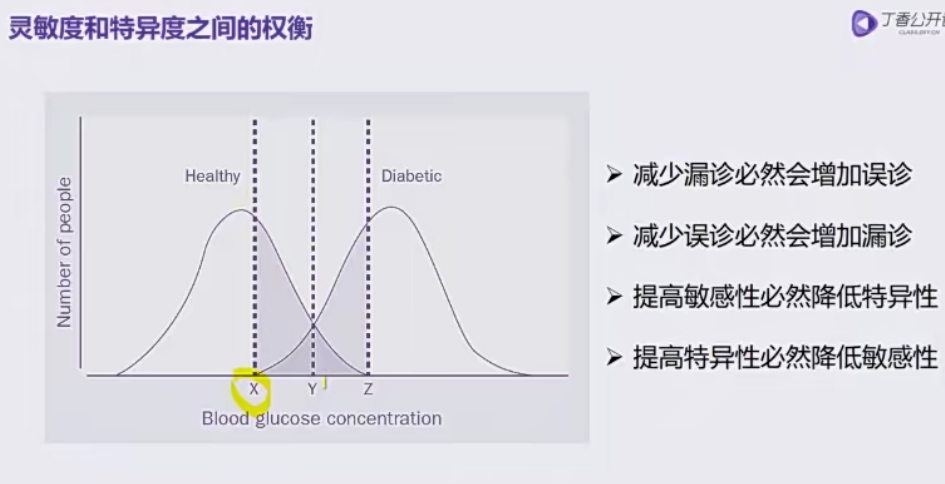
- 敏感度是指诊断试验正确识别有病个体的能力,即真阳性率。它表示在所有真正有病的个体中,被诊断试验正确识别为有病的个体的比例。
特异度是指诊断试验正确识别无病个体的能力,即真阴性率。它表示在所有真正无病的个体中,被诊断试验正确识别为无病的个体的比例。
- 患病率:患病率是指在特定时间内,某人群中患有某疾病的人数所占的比例。例如,如果在一个1000人的社区中,有100人患有某种疾病,那么这种疾病的患病率就是10%。患病率可以反映疾病的流行程度和严重程度,对于制定公共卫生政策和医疗资源分配具有重要意义。
- 预测值:预测值则是指诊断方法对于疾病诊断的准确性。在医学诊断中,预测值通常分为阳性预测值和阴性预测值。阳性预测值是指当诊断方法判断为阳性时,真正患有疾病的人数所占的比例;而阴性预测值则是指当诊断方法判断为阴性时,真正没有患病的人数所占的比例。例如,如果一种诊断方法判断为阳性的患者中,有90%真正患有疾病,那么这种诊断方法的阳性预测值就是90%。

- ROC曲线分析(Receiver Operating Characteristic Curve)(受试者工作特征曲线)是一种用于比较不同诊断试验性能的方法。它通过绘制不同介质下的敏感度和特异度的组合,形成一个曲线图,用于评估诊断试验的整体性能。ROC曲线下的面积(AUC)越大,表示诊断试验的性能越好。
- 凹透镜线(LC曲线)也是一种评估诊断试验性能的方法,它是以1-特异度为横轴,敏感度为纵轴绘制的曲线。与ROC曲线不同,LC曲线更侧重于评估诊断试验在不同介质下的性能变化。当有多种介质或阈值时,可以使用LC曲线来比较不同诊断试验的性能差异。
- 注意:敏感度和特异度是依赖于介质或阈值的,因此在比较不同诊断试验或评估同一诊断试验在不同介质下的性能时,必须指明具体的介质或阈值。此外,对于分类资料(如CT阳性阴性等),由于其介质或阈值只有一个,因此无法绘制ROC曲线或LC曲线,此时只能使用敏感度和特异度来评估诊断试验的性能。
15 ROC分析
ROC曲线分析(Receiver Operating Characteristic Curve)(受试者工作特征曲线)是一种用于比较不同诊断试验性能的方法。它通过绘制不同介质下的敏感度和特异度的组合,形成一个曲线图,用于评估诊断试验的整体性能。ROC曲线下的面积(AUC)越大,表示诊断试验的性能越好。
17 联合诊断(ROC分析)
概述
- 联合诊断的逻辑回归:联合诊断是通过结合多个诊断方法的结果来计算联合概率,以提高诊断效能;
当单个诊断方法的诊断效能不高时,联合诊断可能是一种有效的方法。逻辑回归可以用于计算联合概率,并通过C指数(C statistics)评估诊断效能。 - 生存数据分析中的IDI和NRI:IDI(Integrated Discrimination Improvement)和NRI(Net Reclassification Improvement)是用于评估生存数据预测模型改进程度的指标。
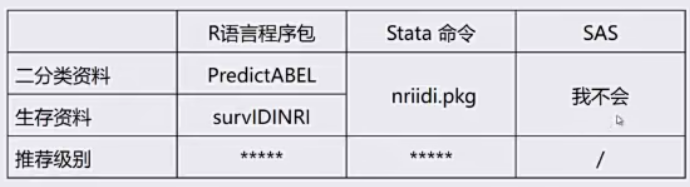
在R语言中,可以使用特定的包(如survIDINRI)来计算IDI和NRI。
计算IDI和NRI需要满足一定的数据条件,包括生存时间、事件指示变量和预测变量等。在使用R语言计算IDI和NRI时,需要替换数据名称和变量名称等,以适应具体的数据集和模型。 - 凡涉及诊断,预测的分析判断都可以使用ROC分析
spss应用
- 整理数据
- 构建逻辑回归方程
- 计算
NRI与IDI的计算(详见R语言笔记)
视频课程这后面录制没录完,不过感觉也差不多了
18 相关与回归的区别与应用
- 线性相关:适用于二元正态分布的统计资料,常用Pearson相关系数表示
- 秩相关:总体分布未知或等级资料等不符合双变量正态分布,用Spearman
- 简单线性回归:因变量为连续变量,自变量仅1个
- 多元线性回归:因变量为连续变量,自变量多个
- 相关:描述两个变量之间是否有关联,多用于横断面研究
- 回归:描述两个变量之间的因果关系,用于可以推论因果关系的临床研究,比如队列研究、病例-对照研究,RCT。
19 简单线性回归与多元线性回归
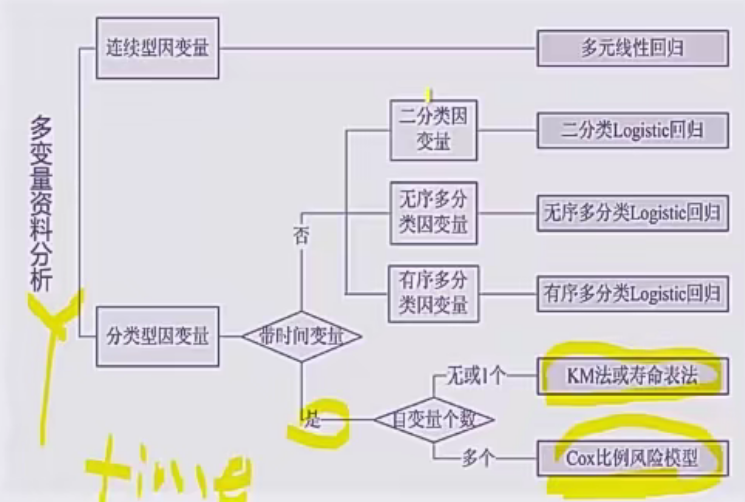
回归分析的方法选择

多变量资料分析
20 Logistic回归模型
- logistic回归模型是一种概率模型,它是以某一事件发生与否的概率P为因变量,以影响P的因素为自变量建立的回归模型,分析某事件发生的概率与自变量之间的关系,是一种非线性回归模型。
- logistic回归模型适用的资料类型:适用于因变量为二项或多项分类(有序、无序)的资料。
分类
- 1、条件Logistic回归模型(适用于配对或配伍设计资料)
- 2、非条件Logistic回归模型(适用于成组设计的统计资料)



应用Logistic回归模型注意事项
- 根据应变量类型,选择合适的Logistic回归模型
对模型汇总自变量的处理:
- 连续性资料:直接纳入
- 无序分类资料:设哑变量
- 等级资料:按等级赋值或设置哑变量
自变量的筛选
- α最大可取0.2(根据需要设定)。当变量较多,先用单因素筛选,同时结合专业考虑
- 样本含量:尽可能多样本,按经验估计至少是自变量的15~20倍
- 对性质相同的自变量进行部分多因素分析(计算相关系数 )
- 将单因素分析有意义及从专业上认为有重要意义的变量,作为候选变量,进行多因素筛选,建立多因素模型。α可以取:0.05.0.1、0.15、0.2。但最好不超过0.1。否则选入一些不重要的变量,所估计的回归系数不稳定
- 考虑是否纳入变量的交互作用项。
21 多因素回归中的变量筛选方法

22 生存分析
关于生存分析几个重要问题
医学统计学的三大回归方法该如何选择
- y为连续变量——线性回归
- y为分类变量——Logistic回归
- time to event——cox回归
生存率和生存概率的区别?

中位生存时间与中位随访时间的区别?
一半人发生结局的时间;随访时间的中位值
KM法与寿命表法该如何选择
- KM法:对生存资料的描述
何为单因素分析?何为多因素分析?
- 单因素:纳入一个自变量
- 多因素:纳入多个自变量
HR该如何理解?何为Crude HR?何为Adjusted HR?
- HR:一组的死亡风险
- Crude HR:未校正的HR,单因素分析出来的HR
- Adjusted HR:校正过后的HR,多因素分析
什么是生存资料,什么是生存分析?
生存资料(time to event)的统计方法称为生存分析(survival analysis),它是将事件的结局和发生这种结局所经历的时间两个因素综合起来分析的一种统计方法,它能够处理截尾数据,并对整个生存过程进行分析或比较。
重要名词解释
终点事件(terminal event)
- 终点事件(terminal event)又称失效事件(failure event)或“死亡”事件(deathevent),泛指标志某种措施失败或失效的事件或反映治疗效果特征的事件,是根据研究目的确定的。如乳腺癌术后死亡、白血病化疗后复发、肾移植术后的肾衰、术后下床活动等,均可作为“死亡”事件。
生存时间(survival time)
- 生存时间(survival time)也是一个广义概念,泛指所关心的某现象的持续时间,即随访观察持续的时间,常用符号t表示。
- 死亡概率

- 生存率


- 生存曲线
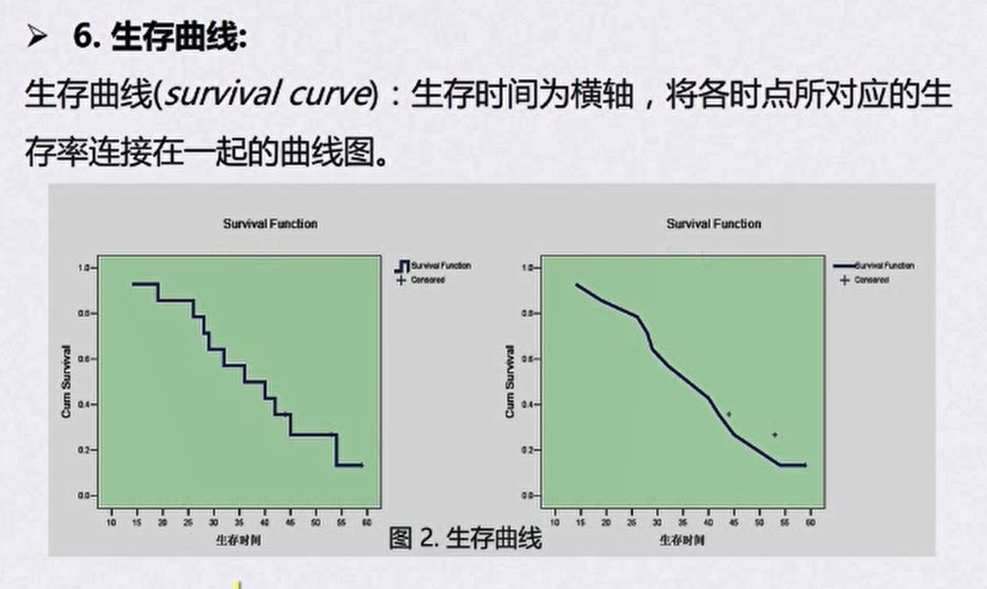
生存分析的基本方法
- 非参数法: 不论资料是什么样的分布类型,只根据样本提供的顺序统计量对生存率进行估计,常用乘积极限法和寿命表法。
- 参数法: 假定生存时间服从于特定的参数分布,根据已知分布的特点对影响生存的时间进行分析,常用指数分布法、Weibul分布法、对数正态回归分析法和对数logistic回归分析法。
- 半参数法:介于参数法和非参数法之间,一般属多因素分析方法,用于探讨生存过程的主要影响因素,其经典方法是Cox比例风险回归模型
生存率的估计与生存曲线——KM法
乘积极限法:
- 又称Kaplan-Meier法,适用于分组生存资料的分析,需要已知魅力患者的生存时间与状态
生存率的估计与生存曲线——寿命表法
寿命表法
- 适用于未分组的生存资料,不需要知道每例患者的生存时间和状态
中位生存时间计算方法——线性内插法
生存曲线的比较——Log-rank检验

23,24 cox回归(比例风险模型)
- 概念:
cox回归可以分析多种因素对时间的影响,而且允许有“截尾”存在,是生存分析中最重要的模型之一;cox回归模型主要用于肿瘤和其他慢性病的预后因素分析,也可以用于一般临床疗效评价和队列病因探索。 
主要用途
- 建立以多个危险因素估计生存或死亡的风险模型,并由模型估计多个危险因素导致死亡的相对危险度RR
- 用已建立的模型,估计患病后随时间变化的生存率
- 用已建立的模型,估计患病后的危险指数,或预后指数PI
应用条件
应用条件
- 已知观察对象的生存时间
- 已知观察对象在事先确定的观察时间内,是否发生某时间的结果
- 自变量可以是计量资料,计数资料或等级资料
等比例风险模型(PH)。指在协变量不同状态的病人的风险在不同的时间保持不变。如:在研究的10年中,糖尿病人心脏病发作的可能性是非糖尿病人的3被,无论在第1年,第2年……都是如此
- 按协变量分组的KM生存曲线,如生存曲线明显交叉,则不满足PH假定
- 将协变量与时间作为交互项引入模型,如果交互项没有统计学意义,则等比例风险成立,若有统计学意义,则不成立。与时间有关的风险称为非比例风险,采用非比例风险模型分析。
检验方法
- 最大似然比检验
- 常用Wald检验,得分检验
分析步骤
因子初步筛选
- 剔除缺失数据较多的因子
- 剔除变异几乎为零的因子
- 对所有的因子逐个作单因素COX模型分析,选择有统计意义的变量作多因素COX模 型分析。此时的α值可以取稍大些,如α=0.1。
拟合多因素模型
- 规定检验水准α,初步的探索性研究 ,可取 α=0.10 或 α=0.15;严谨的、证实性研究,取x=0.05或x=0.01
- 筛选因子方法:前进法、后退法、逐步法。
结果解析与评价
- 模型在一定的检验水准α下,入选哪些因素?
- 入选因素哪些是保护因素,哪些是危险因素?
- 入选因素哪个对因变量影响(贡献)最大?

25 Nomogram(列线图)(见R语言笔记)
26,27,28 倾向性匹配得分PSM
定义
- 通过一定的统计学方法对试验组与对照组进行筛选,使筛选出来的研究对象在某些重要临床特征(潜在的混杂因素)上具有可比性
- 一般是通过某种统计学模型求得每个观测的多个协变量的倾向性得分,再按照倾向性得分是否接近进行匹配
- 最常用的统计模型一般是以分组变量为因变量,其他可能影响结果的混杂因素为协变量构建Logistic回归模型
- 计算每个观测的倾向得分,按照得分大小进行匹配
条件:
- 对照组人数是试验组的4倍以上
- 试验组研究对象都能匹配上
- 可以用PSM的一定可以用回归,但PSM无法代替回归
案例

R语言操作
library(Matchlt)
data(lalonde)
head(lalonde)
f = matchit(treat~re74+re75+educ+black+hispan+age+married+nodegree,data=lalonde, method= "nearest" )
summary(f)
matchdata=match.data(f)
matchdata
library(foreign)
matchdata$id <- 1:nrow(matchdata)
write.dta(matchdata, "./matchdata.dta")
3 条评论
[...]医学统计学二临这学期是一开学就上的医学统计学,谁懂开学半个月不到就开始期中考试的含金量(泪医学统计学我用的课本是生统专业同学的红宝书(超级超级厚,比内科学还厚……)很多不学的,又长又臭,只是因为去年课题组学医学统计学用的所以就将就用了;不建议用红宝书,甚至可以不用书……用书的话人卫就够了。网课我也没听过……感觉确实不需要,临床学的医学统计学真的很基础很基础,只需要理解概念就可以了。爱课上面的PPT[...]
像是数理统计的扩充,感觉对于数模竞赛的大量数据分析题会很有用。
仅仅只是傻瓜统计学(只知套公式不知原理),主要是用来做临床数据挖掘(刚入门的科研民工),配合SPSS和R使用对大量数据进行处理验证相关性和风险偏差什么的